图形学入门（二）：光栅化

光栅化（Rasterize）就是将一些矢量形状转换为位图（Raster Image）形式。经过这样的变换后，这些形状才可以在屏幕上进行显示，也可以被打印机打印出来。

之所以需要这么做，是因为我们的屏幕其实可以被看做一个像素（Pixel）的点阵，程序通过设置每个像素点展示的颜色来展示整体的图像。而我们在计算机中描述一个模型的时候，往往使用了这些模型的顶点坐标来进行描述，例如一个三角形的三个顶点是：$(0,\ 0,\ 0)$、$(0,\ 1,\ 0)$ 和 $(1,\ 0,\ 0)$。那么，在一个 $1920 \times 1080$ 的屏幕上，应该把哪些像素点亮来展示这个三角形呢？这个信息模型本身并没有告诉我们，这就存在一个信息的不匹配，因此我们需要光栅化这一步来将这个图形展示出来。

可以顺便一提的是，「Pixel」是 Picture Element 的缩写，翻译成「像素」相当准确，而「Raster」其实是德语的「屏幕」，所谓「Rasterize」直译过来就是「在屏幕上绘制」。本来非常简单清晰的原意被翻译作「光栅化」，导致这个名字听起来有点吓人。

为了方便后续的讨论，在正式开始之前，我们还需要先声明一些前提条件。一般来说，屏幕上的每个像素并不是一个不可分割的点，但是在我们后续讨论的过程中，认为像素就是屏幕显示的最小单位，一个像素中只能展示一个完整的颜色。而我们认为屏幕就是一个二维的像素数据的数组，大小为 $width \times height$，左下角的坐标为 $(0,\ 0)$，每个像素的宽度为 $1$，任意的一个像素 $(x,\ y)$ 的中心位置在 $(x + 0.5,\ y + 0.5)$ 上，如下图 ¹ 中蓝色的像素的坐标就是 $(2,\ 1)$，其中心点的位置就是 $(2.5,\ 1.5)$。我们要做的，就是将上一篇文章中压缩到标准正方体中的图形绘制到这样的目标上：

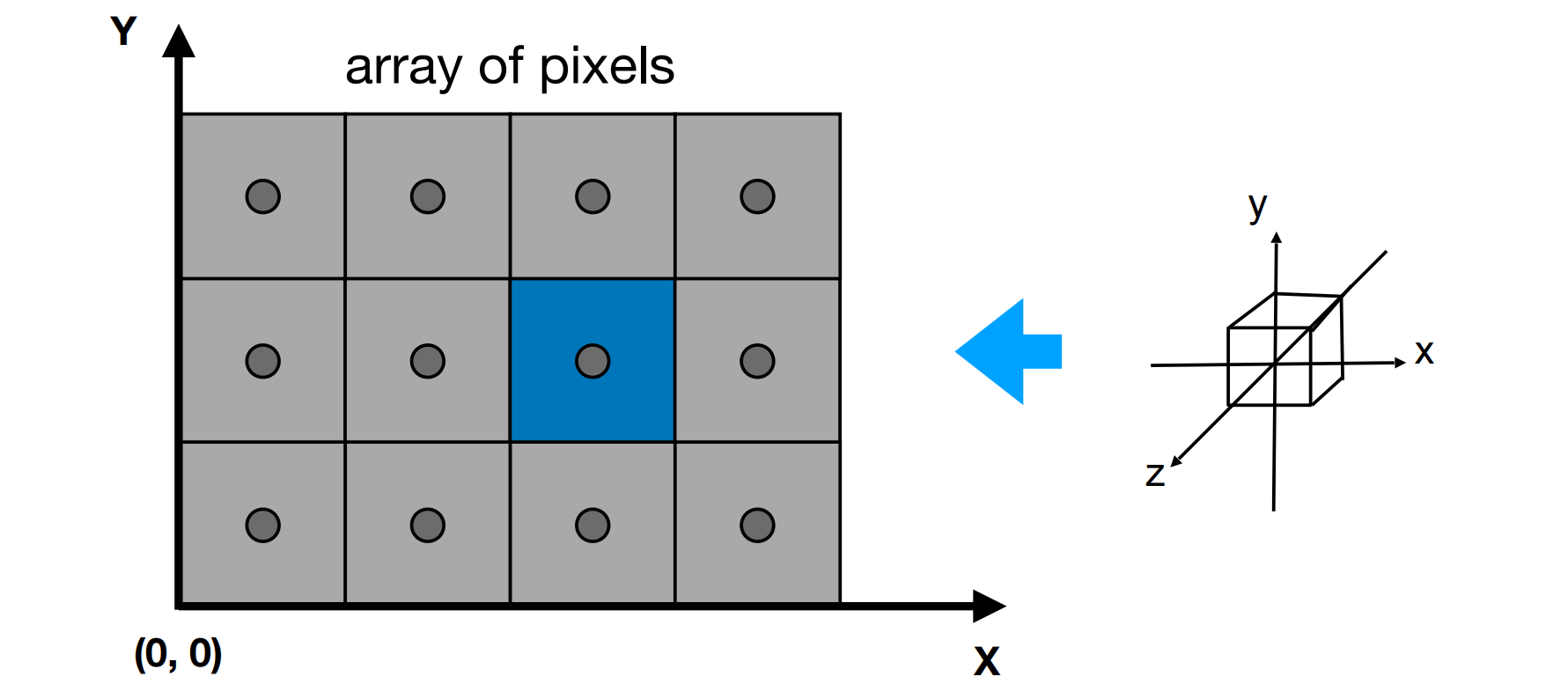
为了操作屏幕上的像素点，我们需要申请一个长度为 $width \times height$ 的数组，数组中的每一个元素都是一个色彩值，一一对应于屏幕上的像素点。然后，我们将绘制的数据记录在这个缓冲区域中，待设置好后再将数据绘制到屏幕上。这块缓冲区域被称为帧缓冲（Frame Buffer）²。

绘制线段 #

让我们先从绘制图形的线框开始，线框的绘制其实就是分别绘制模型的每一条边对应的线段。为了在屏幕上绘制一条线段，我们首先需要计算出线段两个端点坐标在屏幕的位置。在标准正方体内的顶点的 $x$、$y$ 坐标的范围都是 $[-1,\ 1]$，假设我们有一个 $width \times height$ 分辨率的屏幕，我们就需要将其分别变为 $[0,\ width]$ 和 $[0,\ height]$。根据上一篇文章的知识，我们可以很容易知道，我们只需要对顶点坐标应用如下的矩阵变换，就能得到顶点在屏幕空间下的坐标了：

$$ M_{viewport} = \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \newline 0 & \frac{height}{2} & 0 & \frac{height}{2} \newline 0 & 0 & 1 & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix} $$

但是我们很快碰到一个问题，就是我们计算出来的结果是一个浮点数，两点之间是一条连续的线段，但我们最终显示的像素是一个个不可分割的离散元素，这其中存在数据的不匹配：

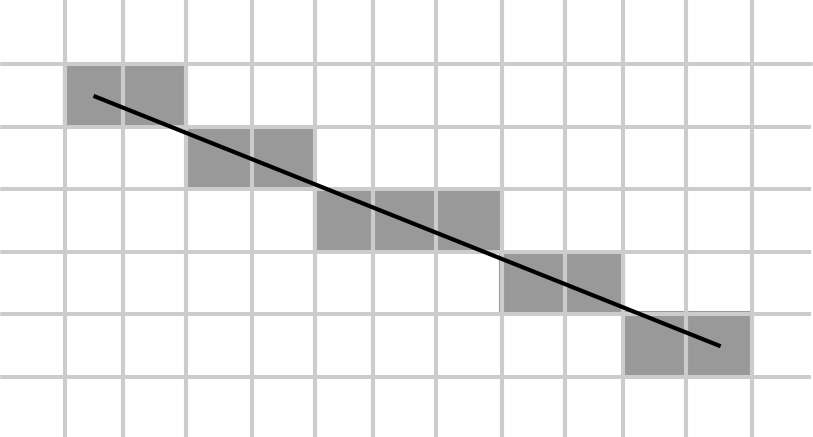
也就是说，我们需要找到一个方法，能让我们用这些离散的点模拟出连续的线，并需要确切知道哪些像素应该点亮，哪些像素不应该点亮。这本质上是一个连续数据的离散化问题。为了将连续的数据离散化，我们要做的事情就是采样（Sampling）。所谓「采样」³，就是对一个连续的函数取一组离散的点上的函数值，例如下图中就是对一个一维函数的采样：

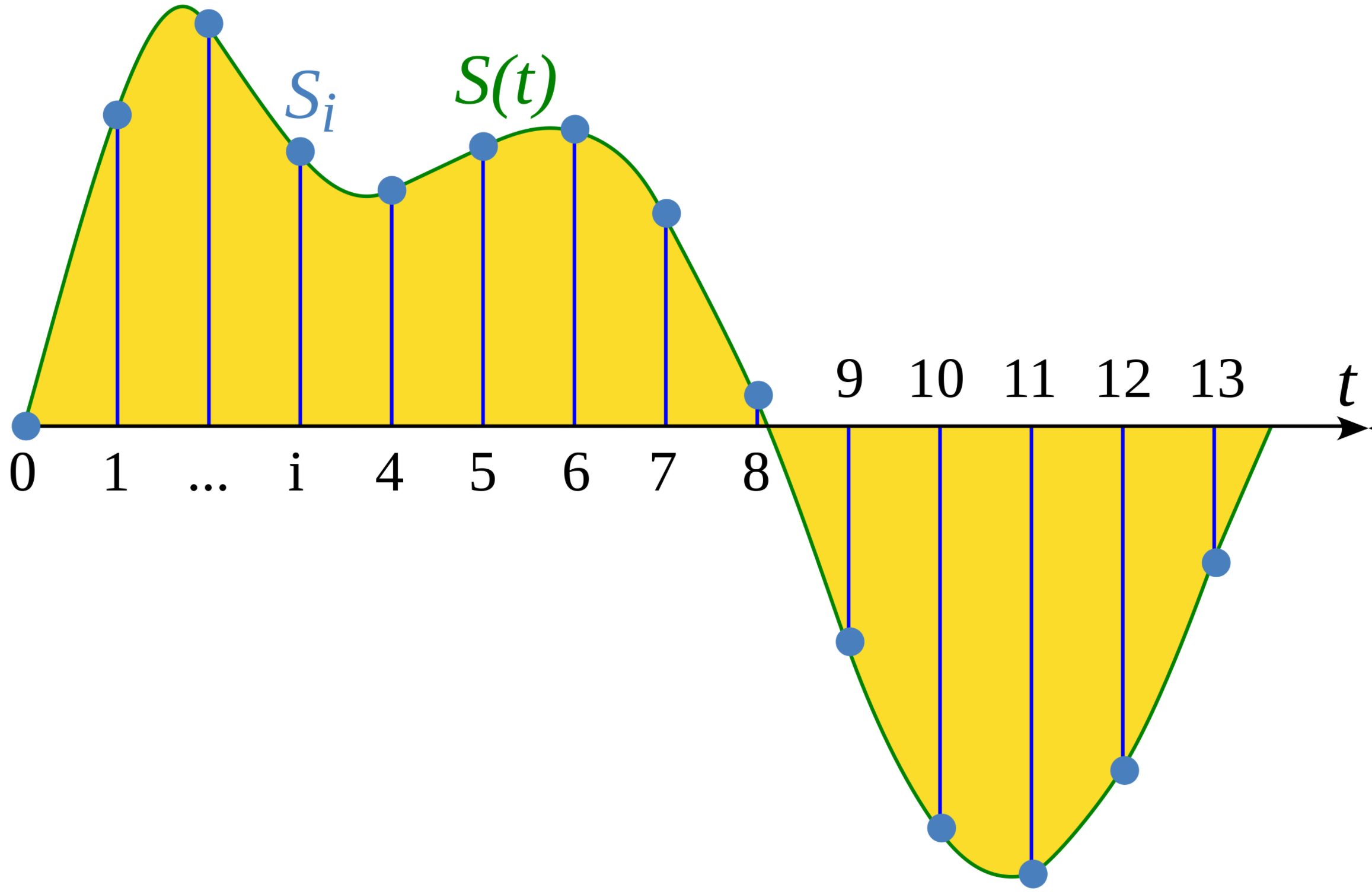
$S(t)$ 是一个关于时间 $t$ 的连续函数，我们每隔一个单位时间进行一次采样，然后就能获得一组离散的函数值，对于输入为 $i$ 的采样点，我们将其值记为 $S_i$。采样是图形学中一个非常常用且重要的做法，我们会对各种各样的东西进行采样，使其便于被计算机处理，例如对时间采样、对面积采样、对体积采样等等。那么对于线段绘制而言，我们是对什么函数进行采样呢？假设我们需要绘制的从 $(x_0,\ y_0)$ 到 $(x_1,\ y_1)$ 的线段，那么，对于线段上任意一点 $(x,\ y)$ 我们有：

$$ \frac{y - y_0}{x - x_0} = \frac{y_1 - y_0}{x_1 - x_0} $$

因此，给定一点 $x$，我们可知：

$$ y = (x - x_0) \ \frac{y_1 - y_0}{x_1 - x_0} + y_0 $$

显然，这就是我们要采样的函数。又由于每个像素点都是不可分割的，因此我们可以简单地将采样的步长设定为 $1$：

for (int x = x0; x <= x1; x++)
  float t = (x - x0) / (float)(x1 - x0)
  int y = y0 * (1 - t) + y1 * t
  draw(x, y)

但在实际使用这个函数进行绘制时，我们会发现一个问题，一旦斜率「过大」（大于 $1$），我们绘制出来的线段就成为了一堆不连续的点，如下图所示（右侧的线段斜率为 $0.5$ 左侧的线段斜率为 $5$）：

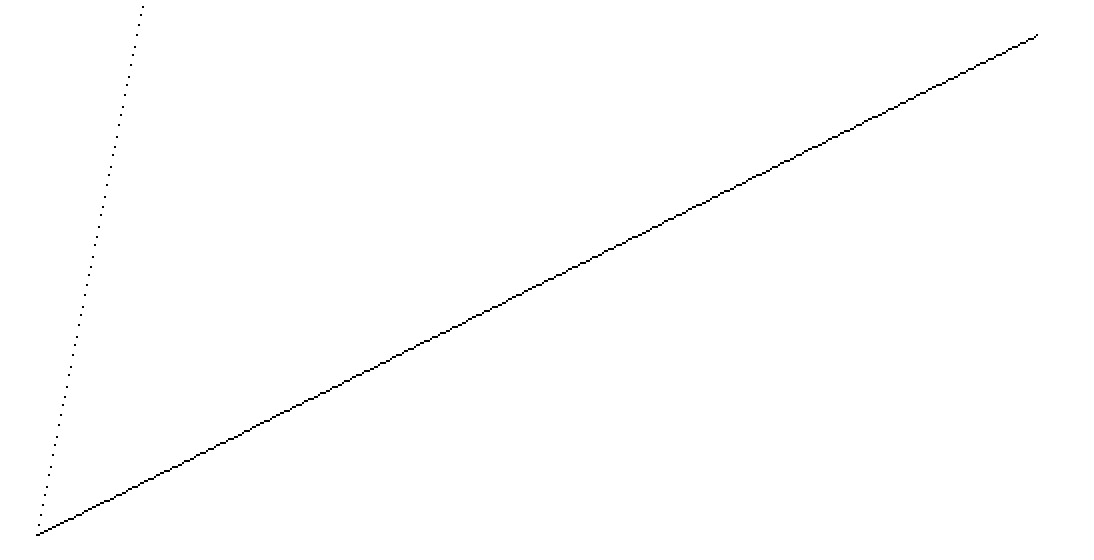
这是因为我们选择使用步进 $x$ 来计算 $y$ 的值，当斜率大于 $1$ 的时候，$y$ 的值就会增长「过快」，导致我们在 $x$ 增长 $1$ 之后，$y$ 增加超过了 $1$，造成了这种不连续的情况。另外，由于我们假定了 $x_0 < x_1$，因此对于从右到左的线段我们也无法进行正常的绘制。为了解决上述问题，我们可以将实现改为这样：

bool steep = abs(x0 - x1) < abs(y0 - y1)

if steep
  swap(x0, y0)
  swap(x1, y1)

if x0 > x1
  swap(x0, x1)
  swap(y0, y1)

for (int x = x0; x <= x1; x++)
  float t = (x - x0) / (float)(x1 - x0)
  int y = y0 * (1 - t) + y1 * t
  if steep
    draw(y, x)
  else
    draw(x, y)

上述的实现正确考虑了线段绘制时端点左右的位置关系，并根据是否斜率大小决定使用 $x$、$y$ 中的哪一个作为步进的标准。

在实际工程中，我们会用到一个更加优化的算法，这个算法（严格来说是一族算法）被称为 Bresenham 直线算法 ⁴，该算法能够将每次的 $y$ 值的计算优化为整型数的累加以提升效率，如果有兴趣可以参考对应的 Wikipedia 词条和 Stack Overflow 上的具体实现。

绘制三角形 #

在知道如何绘制线段之后，我们就可以绘制任意多边形的线框了，但是我们还无法绘制一个填充的图形。在这一节中，我们将讨论如何绘制一个填充的三角形。

为什么只讨论三角形的绘制呢？首先，三角形是最简单的多边形，任何复杂的多边形都能拆成若干个三角形。其次，三角形一定是一个凸多边形，这使得我们可以有简单可行的方式判定一个点是否在三角形内部。而且，三角形稳定性确保了三角形的所有顶点一定会在一个平面上。事实上，我们在游戏中的模型也主要是用三角形来表示的。因此在这里，我们只讨论三角形的绘制方式。

类似于我们在线段绘制的过程中碰到的问题，概念中的图形也是连续的，而由于像素点是离散，因此我们又碰到了将连续数据离散化的问题。我们对此的解决方案依然是采样。对一个图形采样有不同的方式，在这里，我们采用最简单的方式，令每个采样点就是像素的中心位置，根据采样的结果确定一个像素是否在三角形内部，如果一个像素点被认为在三角形的内部，我们之后就将其颜色设置为三角形的颜色。如下图 ¹ 中，我们对左侧的三角形进行采样，中间的图中每一个圆点就是一个采样点，其中红色的点对应的像素就被认为在三角形中，最后我们将这些红色的点对应的像素填充三角形的颜色，我们就可以得到右边的图了：

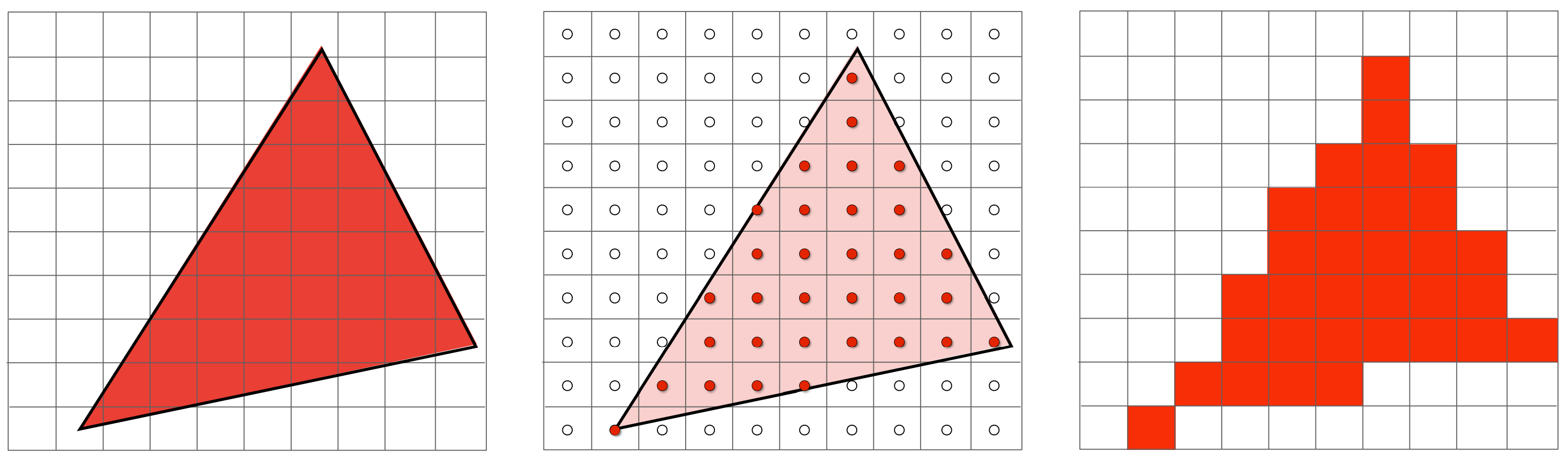
假设我们已经有一个 inside 函数可以确定一个点是否在三角形中，即：

inside(t, x, y) == 1, if point (x, y) in triangle t
inside(t, x, y) == 0, otherwise

那么我们就可以通过简单地遍历屏幕的所有像素，来确定哪些点需要绘制了（注意我们用像素的中心位置来进行判定）：

for (int x = 0; x < width; x++)
  for (int y = 0; y < height; y++)
    if inside(t, x + 0.5, y + 0.5)
      draw(x, y)

那么，我们要怎么判定一个点是否在一个三角形内呢？对于一个三角形来说，这个判断并不困难。首先，我们可以用向量的叉乘结果的正负来判定一个向量在另一个向量的左侧还是右侧。我们知道，在三维空间中，向量的叉乘结果是一个同时垂直于这两个向量的向量。但在二维空间中，我们的出来的却是一个值，这听起来听奇怪的。

假设我们有两个二维向量 $\vec{u} = (u_x,\ u_y)^\mathrm{T}$ 和 $\vec{v} = (v_x,\ v_y)^\mathrm{T}$，那么，我们可以认为它们其实是两个 $z$ 轴方向值为 $0$ 的三维向量 $\vec{u} = (u_x,\ u_y,\ 0)^\mathrm{T}$ 和 $\vec{v} = (v_x,\ v_y,\ 0)^\mathrm{T}$。根据三维空间的叉乘公式 ⁵ 我们可知结果 $\vec{s}$ 的值为：

$$ \vec{s} = \begin{bmatrix} s_x \newline s_y \newline s_z \end{bmatrix} = \vec{u} \times \vec{v} = \begin{bmatrix} u_y v_z - u_z v_y \newline u_z v_x - u_x v_z \newline u_x v_y - u_y v_x \end{bmatrix} = \begin{bmatrix} 0 u_y - 0 v_y \newline 0 v_x - 0 u_x \newline u_x v_y - u_y v_x \end{bmatrix} = \begin{bmatrix} 0 \newline 0 \newline u_x v_y - u_y v_x \end{bmatrix} $$

我们就是用这里的 $s_z = u_x v_y - u_y v_x$ 的结果作为二维空间下向量叉乘的结果，这个结果是一个实数。如果这个值大于 $0$，那么 $\vec{v}$ 在 $\vec{u}$ 的左侧，如果值小于 $0$，则在右侧。对于任意一个三角形 $\triangle_{ABC}$ 而言，假设 $A$、$B$、$C$ 三点逆时针排布，如果同时有：

• $\vec{AP}$ 在 $\vec{AB}$ 的左侧，即 $\vec{AB} \times \vec{AP} > 0$
• $\vec{BP}$ 在 $\vec{BC}$ 的左侧，即 $\vec{BC} \times \vec{BP} > 0$
• $\vec{CP}$ 在 $\vec{CA}$ 的左侧，即 $\vec{CA} \times \vec{CP} > 0$

则点 $P$ 必然在三角形 $\triangle_{ABC}$ 内。而对于任意方式排布的 $A$、$B$、$C$ 三点而言，我们也只需要判定 $\vec{AB} \times \vec{AP}$、$\vec{BC} \times \vec{BP}$、$\vec{CA} \times \vec{CP}$ 三者的结果是否同号即可得知点是否在三角形内。

在实际应用中，每个三角形的面积都不会很大，我们对每一个三角形都遍历屏幕的所有像素显然过于浪费了，我们可以只遍历三角形包围盒，即 $(x_{min},\ y_{min})$ 到 $(x_{max},\ y_{max})$ 中的像素，准确来说，这种包围盒叫做 AABB 包围盒（Axis-aligned bounding boxes）⁶。这样的做法可以极大地减少需要遍历的像素量，下图中左侧的图展示了这个过程，我们仅对蓝色的部分进行采样。当然了，即便采用了这种方法，我们还是不可避免地遍历到无效的像素，如果一个三角形比较狭长，且呈现一种 $45^\circ$ 的斜向布局时会尤为严重。我们可以采用一种更为复杂的遍历方式，来实现真正的只遍历三角形覆盖的像素点。对于任意的三角形，我们都可以将三角形水平切分为两个平底的三角形（或者说是其中一个底边边长为 $0$ 的「平底梯形」）。例如下图中的三角形可以通过一条经过 $P_1$ 的横线将三角形 $\triangle_{P_0 P_1 P_2}$ 切分为 $\triangle_{P_0 P_1 Q}$ 和 $\triangle_{P_1 P_2 Q}$，在切分后，我们就可以对这两个平底三角形分别进行逐行扫描（每一行扫描线的范围就是水平线与左右斜边的交点），整个过程大致如下图中的右图所示：

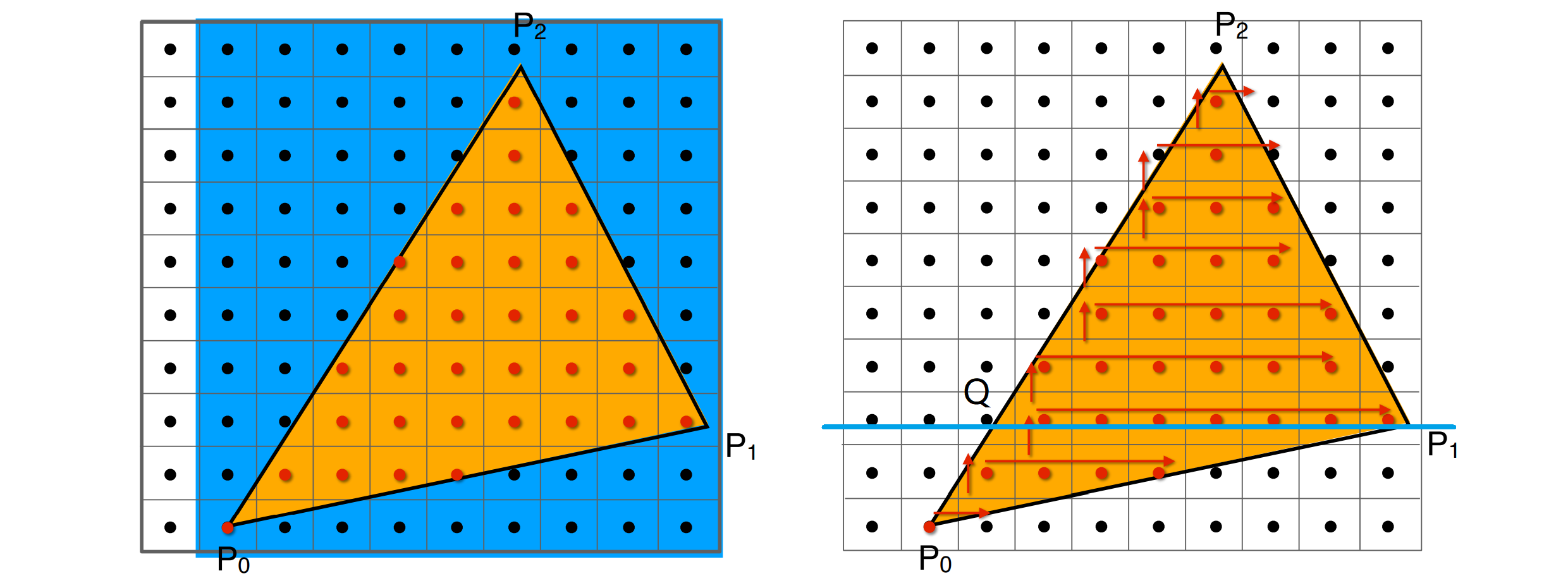
这个过程说起来不难，但实际实现的时候却有很多细节需要考虑，例如拆分三角形要如何拆分？如果三角形本来就是平底三角形如何处理？这里就不列出详细的代码了，有兴趣的话可以参考一下Mini3D 中的 C 语言的实现 ⁷。

遮挡处理 #

当我们能正确绘制一个三角形之后，我们就应该考虑整个场景中所有三角形的绘制了。绘制多个三角形当然不仅仅是将每个三角形依次绘制这么简单，由于一个场景中的三角形之间可能互相遮挡，因此我们想要用某种方法实现靠近相机的三角形遮挡远离相机的三角形的效果。

一个简单的思路就是，我们先绘制离相机远的三角形，然后再绘制离相机近的三角形，这样一来，近处的三角形自然就会覆盖掉远处的三角形了，这个思路正是画家算法 ⁸ 的思路。画家算法的灵感来源于油画的绘制过程，在油画绘制的时候，后被绘制在画布上的元素会覆盖掉下方的元素，最终保持在画布最顶层的元素共同呈现了油画最终的样子：

但是，三角形的排布可能并不总如我们所想的一样存在严谨的前后顺序，例如在下图 ⁹ 中的 $\triangle_P$、$\triangle_Q$、$\triangle_R$ 就互相交叠，无论先绘制哪一个三角形，都无法实现图中的绘制效果：

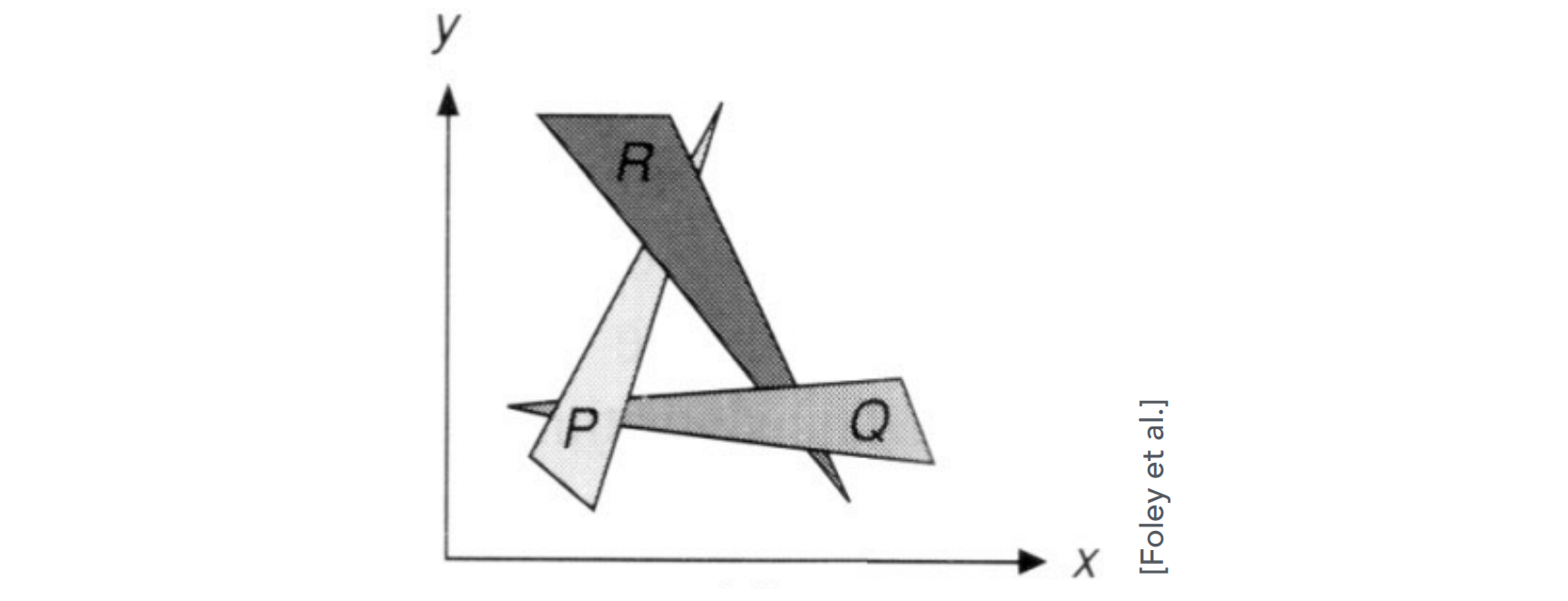
画家算法的局限性促使了深度缓冲 ¹⁰ 技术的发展 ⁸。所谓深度缓冲，其实可以看作是像素级别的画家算法。既然三角形会互相交叠，我们就选取不会互相交叠的单位就可以了，显然，对于屏幕而言，这个单位就是像素了。正如我们最开始声明的一样，我们认为像素不可分割，只能显示一个颜色。

深度缓冲的核心思想是用一块额外的缓冲区域（称为 z buffer）记录每一个像素值当前的最小深度（为方便讨论，我们这里认为离相机近的深度值比较小，且深度值恒为非负数）。首先，我们将 z buffer 中每一个值都初始化为 float.MaxValue，当决定是否要绘制这个点时，我们先比较待绘制点的深度值和 z buffer 中的深度值的大小，如果比之前记录的要小，那么就绘制（将 frame buffer 中对应像素的颜色值替换为当前颜色值），并将当前的深度值记录在 z buffer 中：

foreach (triangle t in scene)
  foreach (sample (x, y, z) in t)
    if z < zbuffer[x, y]
      framebuffer[x, y] = newcolor
      zbuffer[x, y] = z

Z buffer 中记录的数据在归一化后可以被看作一个灰度的颜色值，我们可以直接将这个数据渲染出来。距离相机越近的点对应的 z buffer 中的像素值就越小，也就越接近黑色，反之则越接近白色，如下图 ⁹ 所示：

虽然深度缓冲技术基于深度值能够精确地确定每个像素值的颜色，但是在实际的应用中，由于浮点数的精度问题，我们可能会碰到一个像素点对应的若干个空间上的点深度极为接近甚至一样的情形，在这种情况下，我们在屏幕上绘制这几个点中的哪一个就变得几乎随机了。这种现象被称为 Z Fighting，我们在玩游戏的时候或多或少也会见到如下 ¹¹ 的情况：

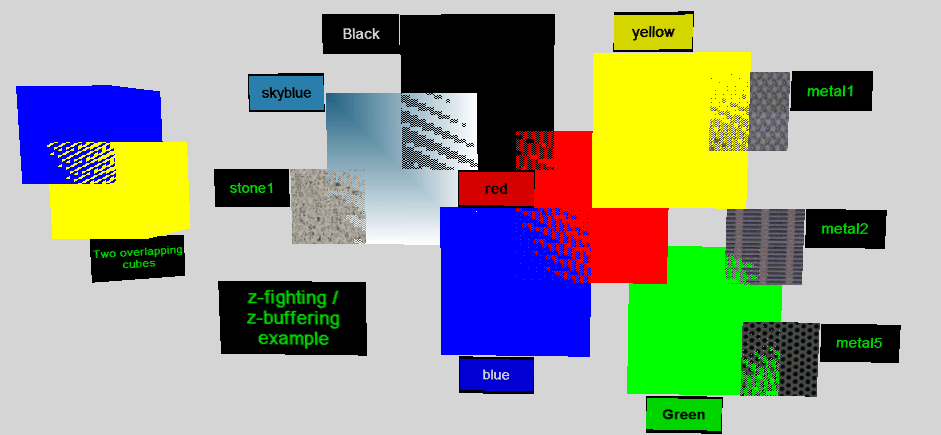
为了减少这些情况，我们可以将模型之间的最小距离限制在一个范围外，避免三角形面的重叠。或者更精确的处理会使用到模板缓冲（Stencil Buffer）¹²，这里就不再赘述，有兴趣可以查阅对应的 Wikipedia 词条。

参考资料 #